一、强度
由医疗质量检测技术展知悉,强度的拉伸试验测试主要用于测定金属材料在拉伸过程中抵抗破坏的能力,是评价材料力学性能的重要指标之一。
1、拉伸试验
拉伸试验测试基于材料力学的基本原理,通过在一定条件下对材料试样施加拉伸载荷,使其产生拉伸变形,直至试样断裂。在试验过程中,记录试样在不同载荷下的变形量,以及试样断裂时的最大载荷,从而计算出材料的屈服强度、抗拉强度等性能指标。
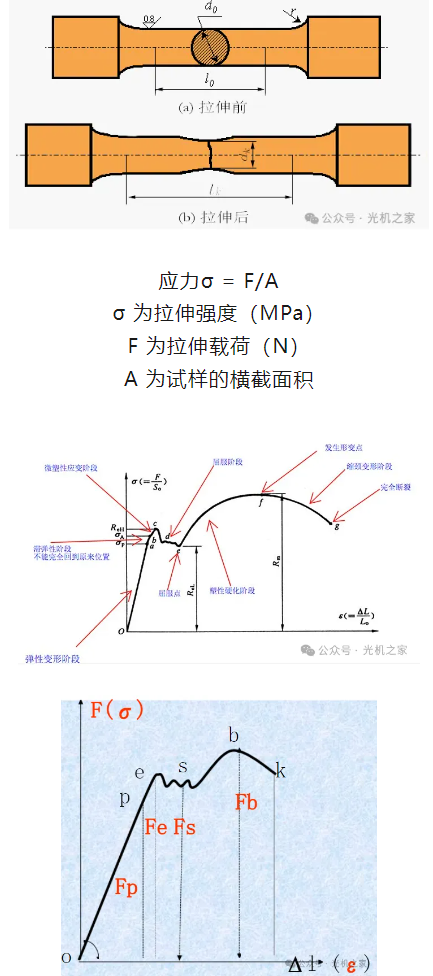
图片来源:光机之家
2、拉钟曲线
屈服强度
屈服强度是金属材料在受到外力作用时,从开始产生塑性变形到完全断裂的过程中所能承受的最大应力值。这个值标志着材料从弹性变形阶段过渡到塑性变形阶段的临界点。
分类
上屈服强度:指试样在发生屈服而力首次下降前的最大应力。
下屈服强度:指当不计初始瞬时效应时,屈服阶段中的最小应力。由于下屈服点的数值较为稳定,因此通常以它作为材料抗力的指标,称为屈服点或屈服强度。
计算公式
对于上屈服强度:R = F / Sₒ,其中F为屈服阶段中力首次下降前的最大力,Sₒ为试样的原始横截面积。
对于下屈服强度:R = F / Sₒ,其中F为不计初始瞬时效应的最小力F,Sₒ为试样的原始横截面积。
单位
屈服强度的单位通常为MPa(兆帕)或N/mm²(牛顿每平方毫米)。
举例
以低碳钢为例,其屈服极限通常为207MPa。当受到大于此极限的外力作用时,低碳钢将会产生永久变形,无法恢复;而小于此极限的外力作用,低碳钢则能够恢复原状。
屈服强度是评价金属材料力学性能的重要指标之一,它反映了材料在受到外力作用时抵抗塑性变形的能力。
抗拉强度
抗拉强度是材料在拉伸载荷作用下抵抗破坏的能力,具体表现为材料在拉伸过程中所能承受的最大应力值。当材料受到的拉伸应力超过其抗拉强度时,材料会发生塑性变形或断裂。
计算公式
抗拉强度(σt)的计算公式为:
σt = F / A
其中,F是试样在断裂前所承受的最大拉伸力(牛顿,N),A是试样的原始横截面积(平方毫米,mm²)。
单位
抗拉强度的单位通常为MPa(兆帕)或N/mm²(牛顿每平方毫米)。1 MPa等于1,000,000牛顿/平方米,也等于1 N/mm²。
影响因素
抗拉强度受到多种因素的影响,包括材料的化学成分、微观结构、热处理工艺、加工方式等。不同的材料具有不同的抗拉强度,因此在实际应用中需要根据材料的力学性能来选择合适的材料。
实际应用
抗拉强度是材料科学和工程领域中非常重要的一个参数,常用于评估材料的机械性能。在结构设计、材料选择、安全评估等方面,抗拉强度都是必须考虑的因素。例如,在建筑工程中,钢材的抗拉强度是决定其能否承受荷载的重要因素;在航空航天领域,轻质高强材料的抗拉强度是保障飞行器安全性的关键。
疲劳强度:
特点
时间上的突发性:金属疲劳破坏往往在短时间内突然发生,没有明显的预兆。
位置上的局部性:疲劳破坏通常发生在应力集中的局部区域。
对环境和缺陷的敏感性:金属疲劳对环境和材料内部的微小缺陷非常敏感,这些缺陷可能加速疲劳过程。
影响因素
应力幅值:应力的大小直接影响金属的疲劳寿命。
平均应力大小:平均应力越大,金属的疲劳寿命越短。
循环次数:金属在循环应力或应变作用下的次数越多,疲劳损伤累积越严重。
预防措施
优化材料选择:选择具有较高疲劳极限的材料。
降低应力集中:通过结构设计或加工方法来降低应力集中,如采用圆角过渡、增加截面尺寸等。
表面处理:对金属表面进行抛光、喷涂等处理,减少表面缺陷,提高疲劳强度。
检测与维护:定期对金属构件进行检测,及时发现并修复裂纹等缺陷;对易产生疲劳的部位进行维护,如更换磨损的零件、加固薄弱环节等。
金属疲劳是一种常见的金属失效模式,具有突发性、局部性和对环境的敏感性等特点。应力幅值、平均应力大小和循环次数是影响金属疲劳的主要因素。
2、塑性:
塑性是指材料在受到外力作用时,当外力超过其弹性极限后,材料产生永久变形而不破裂的特性。这种变形是不可恢复的,即使移除外力,材料也不会恢复到原来的形状。
塑性指标及其计算公式
伸长率(δ)
定义:伸长率是试样在拉伸断裂后标距段的总变形量与原始标距长度之比的百分数。
公式:δ = (L1 – L0) / L0 × 100%
其中,L0是试样的原始标距长度;
L1是试样拉断后的标距长度。
断面收缩率(Ψ)
定义:断面收缩率是试样拉断后缩颈处的横截面积的最大缩减量与原始横截面积的百分比。
公式:Ψ = (F0 – F1) / F0 × 100%
其中,F0是试样的原始横截面积;
F1是试样拉断后颈处截面积。
3、硬度
想要了解更多请前往医疗质量检测技术展
文章来源:光机之家
若涉及侵权,请立刻联系删除
关键字:









